四哥推荐了 Andrea Corbellini 的椭圆曲线加密算法科普系列文章后,在<椭圆曲线加密算法科普系列的作业>和<椭圆曲线加密算法之Sony惨案模拟题>文章中各出了一些作业题目,我花了些时间进行了解答并回复,这里记录一下。
以及,四哥博客文章<椭圆曲线加密算法之Sony惨案模拟题的答案>亦有对我答题的整理。
作业一
设有限域Zp上椭圆曲线如下:
--------------------------------------------------------------------------
y^2 ≡ x^3 + a*x + b (mod p)
p = 10177777
a = 1
b = -1
--------------------------------------------------------------------------
提问:
--------------------------------------------------------------------------
(1) 该椭圆曲线的阶N是多少
(2) 该椭圆曲线用于加密算法时,其n阶循环子群的n是多少
(3) 求一个n阶循环子群生成元G,说一下G在实平面的坐标
(4) 设第3步已求得一个G,且已知两个用户的私钥如下:
dA = 158903
dB = 17
提问,这两个用户的公钥是多少:
HA = ?
HB = ?
说一下HA、HB在实平面的坐标
--------------------------------------------------------------------------
这个作业改一下,比如套ECDSA算法,就可充作CTF赛题。坑爹水果题都能用作CTF赛
题,正经椭圆曲线加密算法题更应该可以。

解答
开始找了挺久的 python 椭圆曲线库,没找到合适的,后面发现 SageMath 这个工具,搜了搜有在线的平台,试着用来解题发现很方便。 SageMath 在线平台可以生成短链,生成了一个,可以访问https://sagecell.sagemath.org/?q=fbjoft查看代码并运行。
from sage.all import *
def largest_prime_factor(number):
# 初始化最大质因数为1
largest_factor = 1
# 从2开始尝试除数
factor = 2
while factor * factor <= number:
if number % factor == 0:
number //= factor
largest_factor = factor
else:
factor += 1
# 如果剩余的数大于1,则该数本身就是最大质因数
if number > 1:
largest_factor = number
return largest_factor
# 定义有限域和椭圆曲线参数
p = 10177777 # 有限域的特征
a = 1 # 椭圆曲线参数a
b = -1 # 椭圆曲线参数b
# 创建椭圆曲线对象
E = EllipticCurve(GF(p), [a, b])
# 计算椭圆曲线的阶
N = E.order()
print("(1)该椭圆曲线的阶N是:", N)
# 选择子群阶(n)
n = largest_prime_factor(N)
print("(2)该椭圆曲线用于加密算法时,其n阶循环子群的n取N最大质因子是:", n)
#辅因子
h = N / n;
#取椭圆曲线任一点P
P = E.random_point()
while h * P == E(0):
P = E.random_point()
G = h*P
# 输出子群基点
print("(3)取椭圆曲线上一点P",P,"得到一个n阶循环子群生成元G,G在实平面的坐标:", G)
dA = 158903
dB = 17
HA = dA*G
HB = dB*G
print("(4)HA:",HA,"HB:",HB)

作业二
ECC公钥(pub.pem)如下:
-----BEGIN PUBLIC KEY-----
MIIBMzCB7AYHKoZIzj0CATCB4AIBATAsBgcqhkjOPQEBAiEA////////////////
/////////////////////v///C8wRAQgAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAA
AAAAAAAAAAAEIAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAHBEEEeb5m
fvncu6xVoGKVzocLBwKb/NstzijZWfKBWxb4F5hIOtp3JqPEZV2k+/wOEQio/Re0
SKaFVBmcR9CP+xDUuAIhAP////////////////////66rtzmr0igO7/SXozQNkFB
AgEBA0IABADEclsh8RJbhCu4meeZlw0gzBz1qTgoiLpK09ATpsF/BpHlr7syDmqf
QDw39Axe+HDZwECCIkHgUgAjiP2kpww=
-----END PUBLIC KEY-----
三组明文如下:
xxd -g 1 message_0.bin
00000000: 54 68 69 73 20 69 73 20 74 68 65 20 66 69 72 73 This is the firs
00000010: 74 20 6d 65 73 73 61 67 65 2e t message.
xxd -g 1 message_1.bin
00000000: 54 68 69 73 20 69 73 20 74 68 65 20 73 65 63 6f This is the seco
00000010: 6e 64 20 6d 65 73 73 61 67 65 2e nd message.
xxd -g 1 message_2.bin
00000000: 54 68 69 73 20 69 73 20 74 68 65 20 74 68 69 72 This is the thir
00000010: 64 20 6d 65 73 73 61 67 65 2e d message.
两组ECDSA签名如下:
xxd -g 1 message_0.sig
00000000: 30 46 02 21 00 90 2e d0 16 f3 b7 58 87 64 85 e3 0F.!.......X.d..
00000010: 3c 6e a3 d4 db 8e f1 a3 3b 7d 83 ce 26 de eb 75 <n......;}..&..u
00000020: 1d 11 7a 82 9d 02 21 00 a3 c5 89 cc 08 4b a4 b5 ..z...!......K..
00000030: 4b f1 84 e2 2b a5 e6 e4 8f 58 21 10 8c 8c 9a 49 K...+....X!....I
00000040: d0 0f 8f cf 4a fc bc b8 ....J...
xxd -g 1 message_1.sig
00000000: 30 46 02 21 00 90 2e d0 16 f3 b7 58 87 64 85 e3 0F.!.......X.d..
00000010: 3c 6e a3 d4 db 8e f1 a3 3b 7d 83 ce 26 de eb 75 <n......;}..&..u
00000020: 1d 11 7a 82 9d 02 21 00 c9 bb 9b 55 86 ef 05 8e ..z...!....U....
00000030: ba 76 3d fe f4 6b 16 09 45 78 01 84 d0 16 09 33 .v=..k..Ex.....3
00000040: 45 f8 71 fc 1a 65 7a 45 E.q..ezE
sha512sum message_0.bin message_1.bin message_2.bin message_0.sig message_1.sig
fd8b4f3ab120efcd6bed61028c2a0b026f5d676535621339d0ed085313ae482cbfae15885e56295939393e78afb11118f0cc89caeba55d65172b870f3c6bb7fd message_0.bin
4ec0b587154fc85b7c28ad5b9f22225817027434b3b26ed895359643deba1e80b4cce0a1181a40a411e94cce88742489349e3f4960090e0e07b1c4e85cdd0b04 message_1.bin
8109b25d7fdaf1374933ae02aefe81dc787a7cec5323eeff51419770f96f2b9066f512dfb36e67dfd29e718e465f30129c26ad2fdc1f6b2398a0abd60f7d31dd message_2.bin
d57f19dd89ba91cf2498551dafa8968ddb66608dd114bd5315e3fed47db244d39e51836fb79f284388c69c03d8c5164da63dcd002883881222b120b3ea2c7c21 message_0.sig
e4c2eab10a86acea580156ba28ca3ff4dab0e4a426b1b2cb1fca7c84c874a599887ecf218afd9785b91bc63fa4a8b055ffcdfcb09d88ced56945909f23654418 message_1.sig
已知k值固定,ECDSA签名数据由类似下列OpenSSL命令生成:
openssl dgst -sha512 -sign priv.pem -out msg.sig msg.bin
验证签名命令类似:
openssl dgst -sha512 -verify pub.pem -signature msg.sig msg.bin
openssl version
OpenSSL 3.0.2 15 Mar 2022 (Library: OpenSSL 3.0.2 15 Mar 2022)
题目要求
a) 参照Sony惨案还原k值、ECC私钥
b) 用还原得到的k值、ECC私钥对message_0.bin生成ECDSA签名message_0_other.sig,
应与message_0.sig完全相同
c) 用还原得到的k值、ECC私钥对message_2.bin生成ECDSA签名message_2.sig,用已
知ECC公钥验证ECDSA签名
整个题目完整模拟了Sony惨案,攻击者获取两份用同样k签名过的PS3游戏,最终还原
了Sony的ECC私钥,进而对第三方游戏进行ECDSA签名,使之可运行在PS3上。
所以已知数据在此:
https://scz.617.cn/misc/SonyECCChallenge.7z
解答
第一题直接套公式,第二题和第三题的话,尝试了下用 ecdsa 库来搞很方便,可以设置 k 和 ECC 私钥。
提取公钥信息
bin4re@wsl:~/crypto/SonyECCChallenge$ openssl ec -in pub.pem -pubin -text -noout
read EC key
Public-Key: (256 bit)
pub:
04:00:c4:72:5b:21:f1:12:5b:84:2b:b8:99:e7:99:
97:0d:20:cc:1c:f5:a9:38:28:88:ba:4a:d3:d0:13:
a6:c1:7f:06:91:e5:af:bb:32:0e:6a:9f:40:3c:37:
f4:0c:5e:f8:70:d9:c0:40:82:22:41:e0:52:00:23:
88:fd:a4:a7:0c
Field Type: prime-field
Prime:
00:ff:ff:ff:ff:ff:ff:ff:ff:ff:ff:ff:ff:ff:ff:
ff:ff:ff:ff:ff:ff:ff:ff:ff:ff:ff:ff:ff:fe:ff:
ff:fc:2f
A: 0
B: 7 (0x7)
Generator (uncompressed):
04:79:be:66:7e:f9:dc:bb:ac:55:a0:62:95:ce:87:
0b:07:02:9b:fc:db:2d:ce:28:d9:59:f2:81:5b:16:
f8:17:98:48:3a:da:77:26:a3:c4:65:5d:a4:fb:fc:
0e:11:08:a8:fd:17:b4:48:a6:85:54:19:9c:47:d0:
8f:fb:10:d4:b8
Order:
00:ff:ff:ff:ff:ff:ff:ff:ff:ff:ff:ff:ff:ff:ff:
ff:fe:ba:ae:dc:e6:af:48:a0:3b:bf:d2:5e:8c:d0:
36:41:41
Cofactor: 1 (0x1)
提取r和s
bin4re@wsl:~/crypto/SonyECCChallenge$ openssl asn1parse -in message_0.sig -inform DER
0:d=0 hl=2 l= 70 cons: SEQUENCE
2:d=1 hl=2 l= 33 prim: INTEGER :902ED016F3B758876485E33C6EA3D4DB8EF1A33B7D83CE26DEEB751D117A829D
37:d=1 hl=2 l= 33 prim: INTEGER :A3C589CC084BA4B54BF184E22BA5E6E48F5821108C8C9A49D00F8FCF4AFCBCB8
bin4re@wsl:~/crypto/SonyECCChallenge$ openssl asn1parse -in message_1.sig -inform DER
0:d=0 hl=2 l= 70 cons: SEQUENCE
2:d=1 hl=2 l= 33 prim: INTEGER :902ED016F3B758876485E33C6EA3D4DB8EF1A33B7D83CE26DEEB751D117A829D
37:d=1 hl=2 l= 33 prim: INTEGER :C9BB9B5586EF058EBA763DFEF46B160945780184D016093345F871FC1A657A45
sha512信息
bin4re@wsl:~/crypto/SonyECCChallenge$ sha512sum message_0.bin
fd8b4f3ab120efcd6bed61028c2a0b026f5d676535621339d0ed085313ae482cbfae15885e56295939393e78afb11118f0cc89caeba55d65172b870f3c6bb7fd message_0.bin
bin4re@wsl:~/crypto/SonyECCChallenge$ sha512sum message_1.bin
4ec0b587154fc85b7c28ad5b9f22225817027434b3b26ed895359643deba1e80b4cce0a1181a40a411e94cce88742489349e3f4960090e0e07b1c4e85cdd0b04 message_1.bin

#message_0.bin sha512 = 0xfd8b4f3ab120efcd6bed61028c2a0b026f5d676535621339d0ed085313ae482cbfae15885e56295939393e78afb11118f0cc89caeba55d65172b870f3c6bb7fd
#message_1.bin sha512 = 0x4ec0b587154fc85b7c28ad5b9f22225817027434b3b26ed895359643deba1e80b4cce0a1181a40a411e94cce88742489349e3f4960090e0e07b1c4e85cdd0b04
n = 0xfffffffffffffffffffffffffffffffebaaedce6af48a03bbfd25e8cd0364141
z1 = 0xfd8b4f3ab120efcd6bed61028c2a0b026f5d676535621339d0ed085313ae482c
z2 = 0x4ec0b587154fc85b7c28ad5b9f22225817027434b3b26ed895359643deba1e80
s1 = 0xA3C589CC084BA4B54BF184E22BA5E6E48F5821108C8C9A49D00F8FCF4AFCBCB8
s2 = 0xC9BB9B5586EF058EBA763DFEF46B160945780184D016093345F871FC1A657A45
r = 0x902ED016F3B758876485E33C6EA3D4DB8EF1A33B7D83CE26DEEB751D117A829D
k = ((z1-z2)*pow(s1-s2,-1,n))%n
d = (pow(r,-1,n)*(s1*k - z1))%n
print(hex(k))
print(hex(d))
import ecdsa
import binascii
import hashlib
ecc_pri = ecdsa.SigningKey.from_string(binascii.unhexlify('60e89fd3bec9c5184ff8b72883bb1989f5504a112f8521eb03258f4171af0c7e'), curve=ecdsa.SECP256k1)
with open('message_2.bin', 'rb') as file:
file_content = file.read()
file_sign = ecc_pri.sign(file_content, k=0x90a0b0c0d0e0f101259f2ae83a986c3b989d814fa02e8eac37c9c7c5b255620, hashfunc=hashlib.sha512, sigencode=ecdsa.util.sigencode_der)
with open('message_2.sig','wb') as f:
f.write(file_sign)
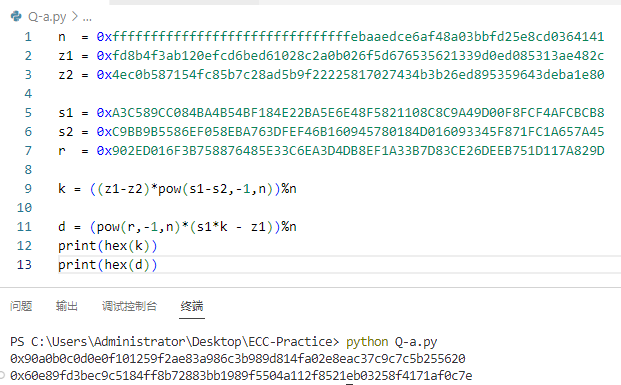


scz回复
经四哥提醒,sagemath 有直接求最大质因子的函数 factor(N)[-1][0],不用自己写,迭代下代码,更简洁了。
from sage.all import *
# 定义有限域和椭圆曲线参数
p = 10177777 # 有限域的特征
a = 1 # 椭圆曲线参数a
b = -1 # 椭圆曲线参数b
# 创建椭圆曲线对象
E = EllipticCurve(GF(p), [a, b])
# 计算椭圆曲线的阶
N = E.order()
print("(1)该椭圆曲线的阶N是:", N)
# 选择子群阶(n)
n = factor(N)[-1][0]
print("(2)该椭圆曲线用于加密算法时,其n阶循环子群的n取N最大质因子是:", n)
#辅因子
h = N / n;
#取椭圆曲线任一点P
P = E.random_point()
while h * P == E(0):
P = E.random_point()
G = h*P
# 输出子群基点
print("(3)取椭圆曲线上一点P",P,"得到一个n阶循环子群生成元G,G在实平面的坐标:", G)
dA = 158903
dB = 17
HA = dA*G
HB = dB*G
print("(4)HA:",HA,"HB:",HB)
总结
作业一中的题目我使用在线 SageMath 给做了,在做题的过程加深了对 Andrea Corbellini 的椭圆曲线加密算法科普系列文章里公式推导的理解,更细致一步思考了文章里的一些节段的主题,题目就对应系列文章里如何先找一个大质数再找基点的部分。完成解题才感到只读文章得到的认知还很浅,做题写代码才发现自己把 NP=0 => nhP=0 里面的P理解为基点了,因为上面示例取 P 为基点,其实P是椭圆曲线上任意一点。
相比之下作业二的索尼惨案的解题要简单得多,知道怎么写模 n 下求幂就行了,比如 pow(p,-1,n),然后就是找对 python 库,试了下 ecdsa 库来解题很方便。大部分时间花在验证上面了,对 ecdsa 理解不到位,对 openssl 的签名的理解存在偏差,比如 k 值 openssl 每次签名都是随机生成的,一开始发现时候我还很惊讶怎么同一个文件每次的签名结果都还不一样。ecdsa 的话,可以很方便地用代码设置 k 值和 ecc 私钥,随后生成证书或者签名文件。